硬币悖论

问题

一个硬币围绕另一个硬币无滑动的滚动，从上方滚到下方时到底旋转了几圈。

滚过的路径只有半个圆周，但是外面的硬币却旋转了一圈。

定量研究

圆周运动

定义

质点在以某点为圆心半径为r的圆周上运动，即质点运动时其轨迹是圆周的运动叫“圆周运动”。它是一种最常见的曲线运动。例如电动机转子、车轮、皮带轮等都作圆周运动。

描述

匀速圆周运动的特点：轨迹是圆，角速度，周期，线速度的大小(注：因为线速度是矢量,”线速度”大小是不变的，而方向时时在变化)和向心加速度的大小不变，且向心加速度方向总是指向圆心。

线速度定义：质点沿圆周运动通过的弧长$\Delta {L}$与所用的时间$\Delta {t}$的比值叫做线速度，或者角速度与半径的乘积。$v=\frac{\Delta {L}}{\Delta {t}} $

线速度的物理意义：描述质点沿圆周运动的快慢，是矢量。

角速度的定义:半径转过的弧度（弧度制:$360^{\circ} = 2\pi $）与所用时间$t$的比值。（匀速圆周运动中角速度恒定）$\omega =\frac{\Delta \theta }{\Delta t} $

周期的定义：作匀速圆周运动的物体,转过一周所用的时间。$T=\frac{2\pi r}{v} $

频率：单位时间内完成圆周运动的圈数。$f=\frac{1}{T} $

转速的定义：作匀速圆周运动的物体，单位时间所转过的圈数。$n=\frac{N}{t} $

各个物理量之间的公式关系如下：

$$\left\{\begin{matrix}v=\frac{2\pi r}{T} =2\pi fr=2\pi nr \\ \omega =\frac{2\pi }{T} =2\pi f=2\pi n \\ v=\omega r \\ T=\frac{1}{f} \end{matrix}\right.$$

速度的叠加

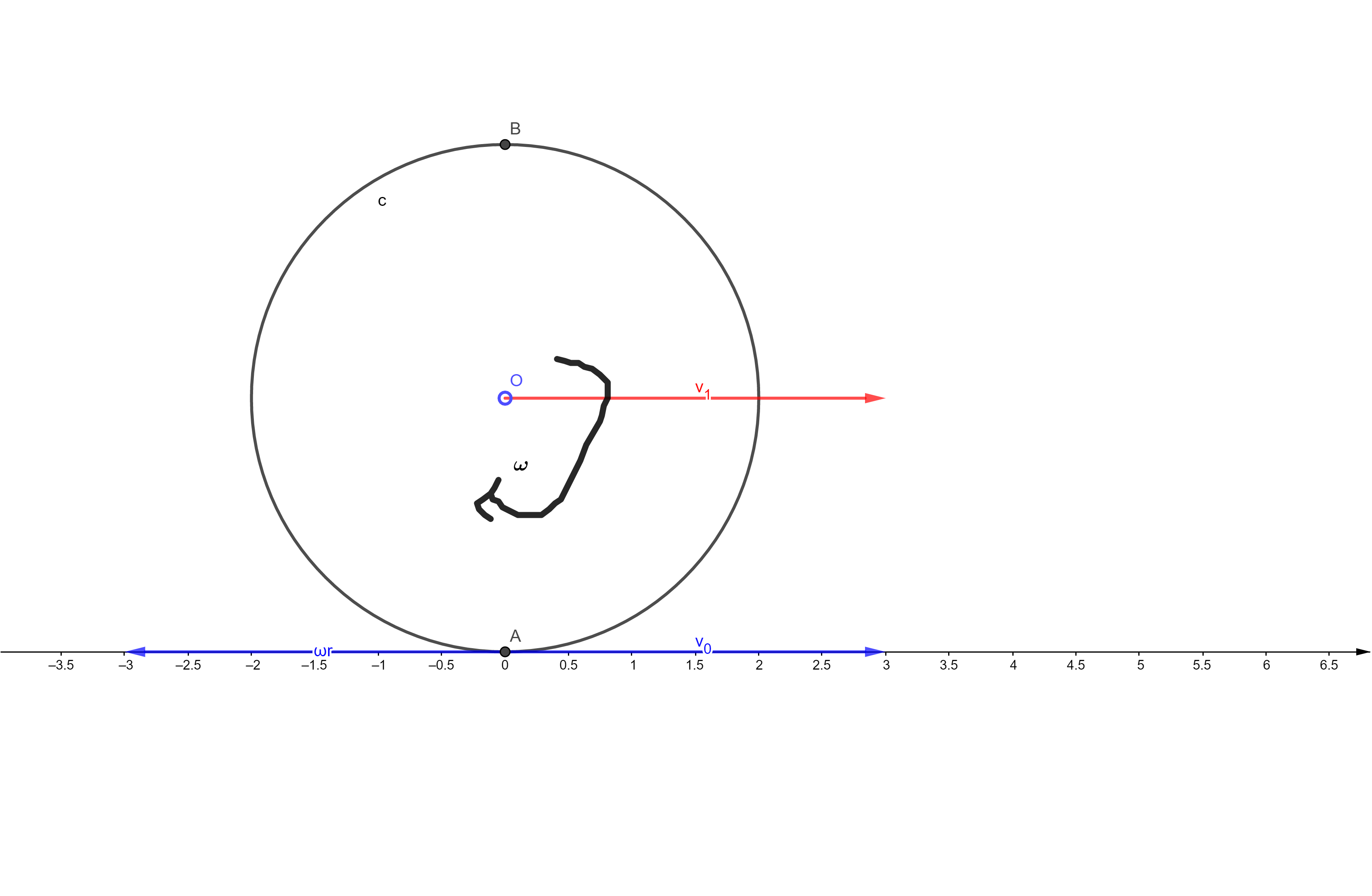
图中贴着地面的点(A点),一方面跟着圆心走速度为$v_0$,另一方面还有一个向后转动的速度为$\omega r$,所以这个点的速度为$v_0$和$\omega r$做差,这一时刻A点为瞬心(即速度等于地面的速度为零)

所以$v_0-\omega r=0$

研究

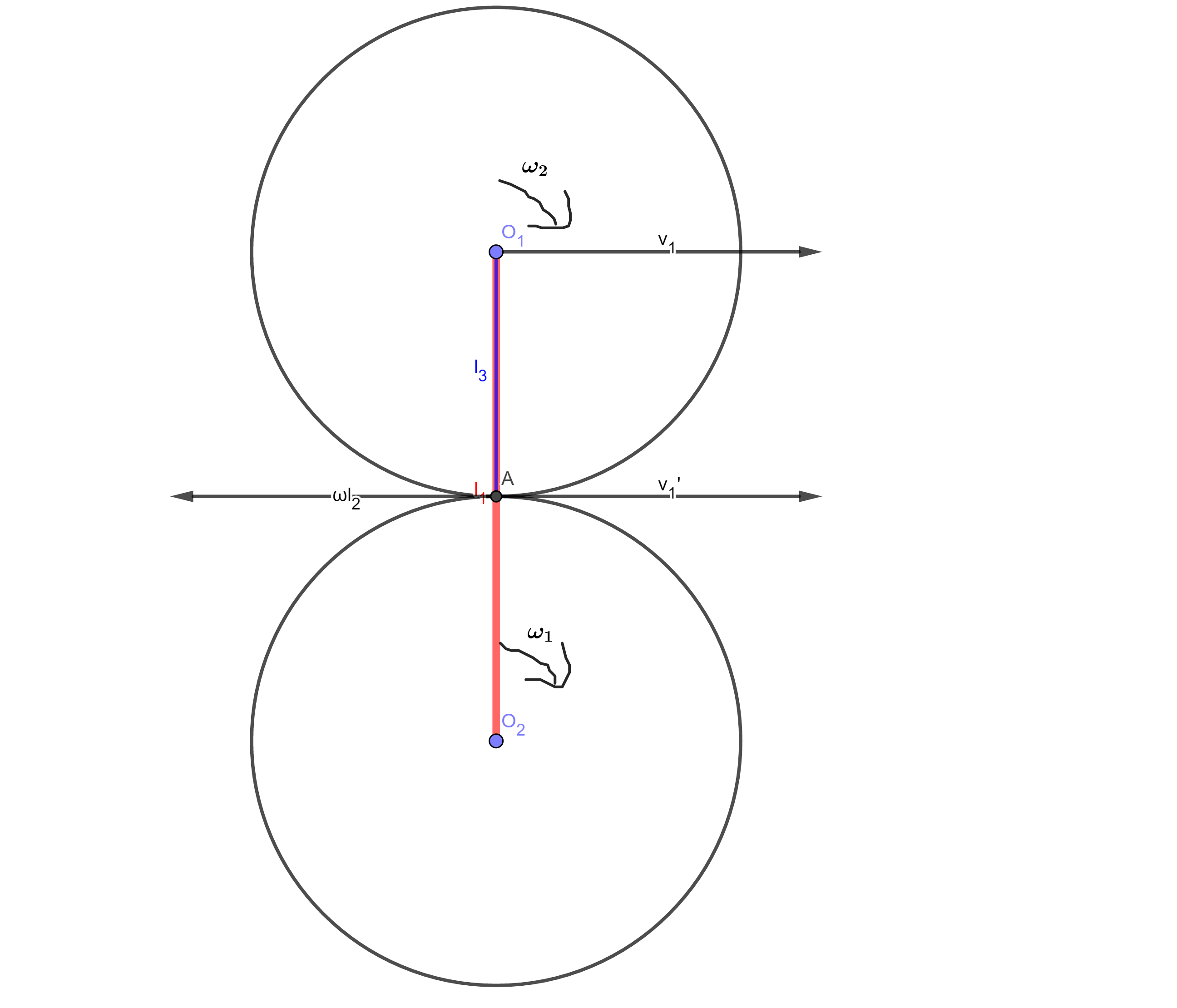
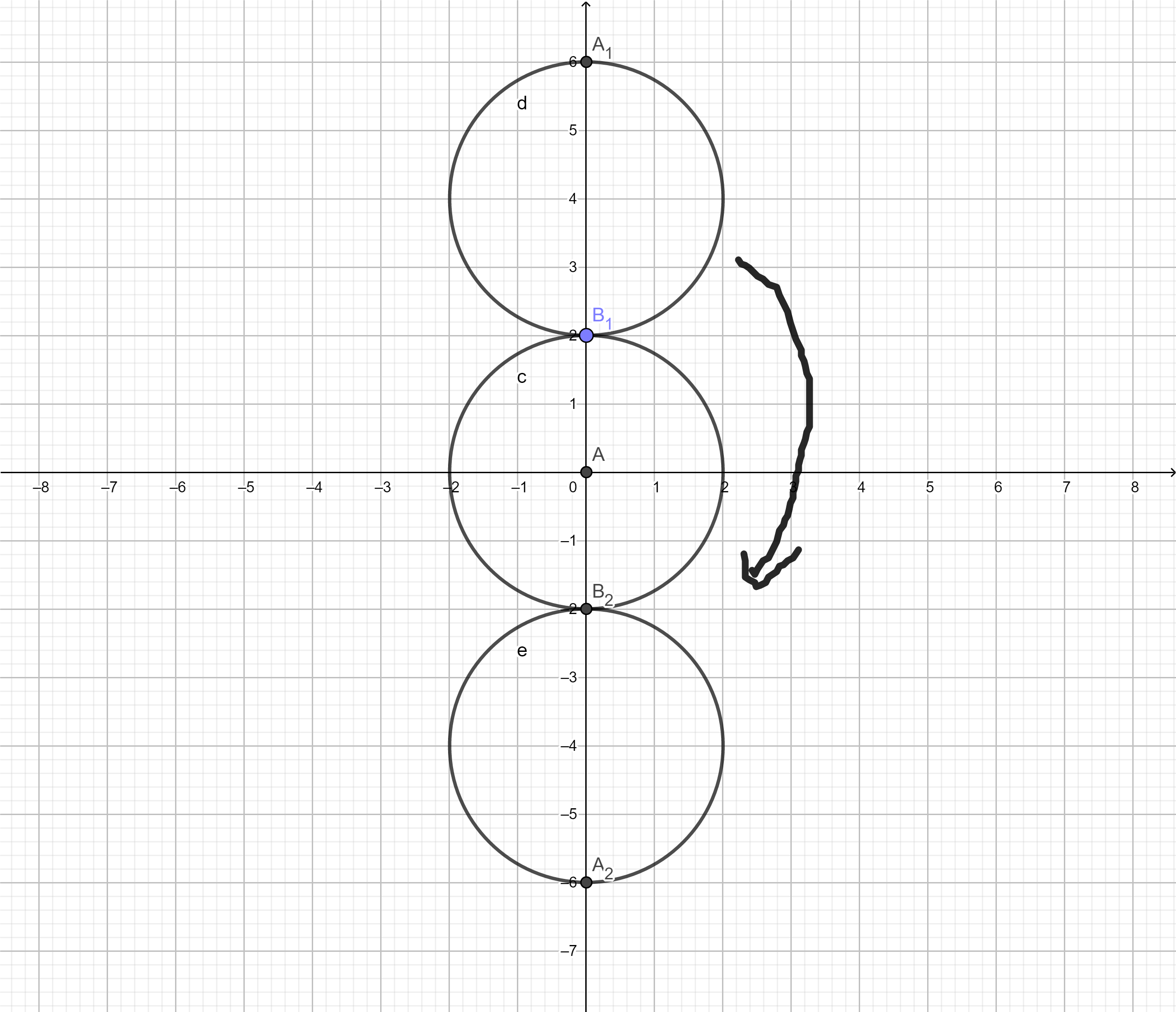
如图所示圆$O_2$不动,因为圆$O_1$在转动,所以连线$O_1 O_2$也在转动,设角速度为$\omega_1$,同时设$O_1 O_2$为$l_1$,$O_1$与两圆的接触点$A $ 的距离为$l_2$,圆$O_1$绕$l_2$旋转的角速度为$\omega _2$.

所以$O_1$点有一个速度为$v_1=\omega_1 l_1$,瞬心$A$点有一个向前速度$v_1’=v_1=\omega_1 l_1$,和一个向后转动的速度为$\omega_2 l_2$.

同时因为$A$点为瞬心,所以$v_A=\omega_1 l_1-\omega_2 l_2$=0

所以$\omega_1 l_1=\omega_2 l_2$,设连线转动角度(公转角度)为$\theta _1=\omega_1 t$,另一圆转过的角度(自转角度)为$\theta _2=\omega_2 t$

由上得

$$\frac{\theta _1}{\theta _2}=\frac{\omega_1 t}{\omega_2 t}=\frac{\omega_1}{\omega_2}=\frac{l_2}{l_1}$$

因为本题中$l_1=2 l_2$,所以$2\theta _1=\theta _2$,即滚过的路径只有半个圆周，但是外面的硬币却旋转了一圈。

总结

当一个圆绕着另一个圆无滑动滚动时

$$\frac{\theta _1}{\theta _2}=\frac{l_2}{l_1}$$

(公转角度) $\theta _1$ (自转角度) $\theta _2$

(两圆心连线) $l1$ (旋转圆半径) $l_2$